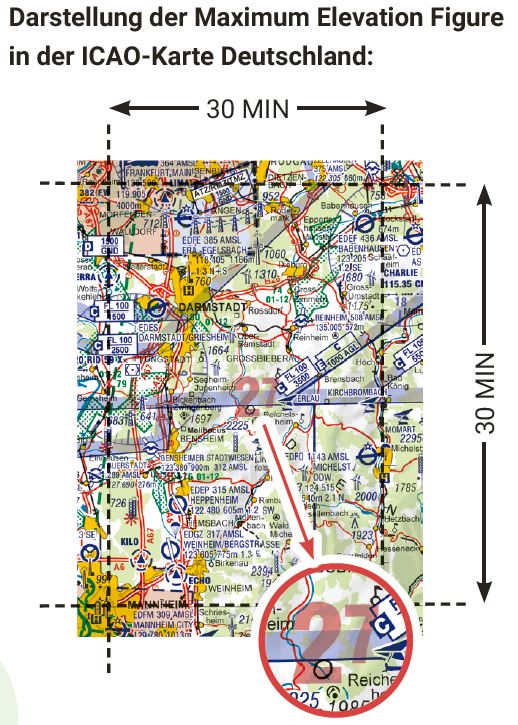
Die fett gedruckten roten Zahlen auf der ICAO-Karte stellen die Maximum Elevation Figure dar. Was bedeuten sie?
 Maximum Elevation Figure lässt sich übersetzen mit „größter Höhenwert“. Für die Ermittlung dieses Wertes gibt es zwei Rechenwege: die Höhenpunkt- und die Hindernisauswertung.
Maximum Elevation Figure lässt sich übersetzen mit „größter Höhenwert“. Für die Ermittlung dieses Wertes gibt es zwei Rechenwege: die Höhenpunkt- und die Hindernisauswertung.
Höhenpunktauswertung
Es wird die Landschaftserhebung (Höhenpunkt) bezogen auf den mittleren Meeresspiegel verwendet. In unserem Beispiel beträgt die Höhe der Landschaft 2331 ft AMSL.
Auf diesen Höhenpunkt wird ein fiktives Hindernis von 328 ft (100 m) Höhe über Grund gesetzt. Grund für diesen fiktiven Wert ist der, dass Hindernisse bis 100 m nicht in der ICAO-Karte eingetragen werden.
Anschließend wird darauf noch ein Sicherheitszuschlag für etwaige Luftdruckänderungen und Einstellfehler am Höhenmesser von 30 ft gepackt.
Die Summe aus diesen drei Werten wird auf den nächsten 100 ft-Wert aufgerundet.
2331 ft + 328 ft + 30 ft = 2689 ft
Aufgerundet: 2700 ft AMSL
Hindernisauswertung
Es wird die Höhe eines bekannten Hindernisses verwendet, welches markant aus der Landschaft herausragt. In unserem Beispiel beträgt die Hindernishöhe 2463 ft AMSL.
Darauf wird ein Sicherheitszuschlag für etwaige Luftdruckänderungen und Einstellfehler am Höhenmesser von 60 ft gegeben.
Die Summe aus diesen beiden Werten wird auf den nächsten 100 ft-Wert aufgerundet.
2463 ft + 60 ft = 2523 ft
Aufgerundet: 2600 ft AMSL
Hinweis: Für die Angabe auf der ICAO-Karte Deutschland und den V500-Karten wird übrigens der höhere der errechneten Werte verwendet. Eine Erklärung inkl. der Rechenwege findet sich jeweils auf der Karten-Rückseite
Dazu gibt es im PPL Fragenkatalog folgende Frage:
Bei einem Hindernis mit der Höhe von 2850 ft AMSL ergäbe sich welche Maximum Elevation Figure? Mit dem Rechenweg der Hindernisauswertung kann das Ergebnis wie folgt errechnet werden:
Hindernishöhe 2850 ft AMSL + Zuschlag 60 ft = 2910 ft AMSL
Aufgerundet: 3000 ft AMSL
Welche Bedeutung hat die Maximum Elevation Figure für den Piloten in der Praxis?
Gleich zu Beginn das Wichtigste: die Maximum Elevation Figure ist nicht mit der Sicherheitsmindesthöhe gleichzusetzen. Aber sie hilft Piloten in der Planung ihrer Flugrouten und vor allem in Situationen, in denen vom geplanten Flugkorridor abgewichen werden muss.
Bei der Planung eines Fluges muss die Sicherheitsmindesthöhe berücksichtigt werden. Bei der Ermittlung dieser unterstützt die MEF.
Wenn eine MEF von 13 angegeben ist, ist in diesem Rechteck von 30 x 30 Minuten, gerechnet auf dem Längen- und Breitenkreis kein natürliches oder künstliches Hindernis höher als 1.300 ft. Dieser Wert wurde aufgerundet auf den nächsthöheren Hunderter-Wert.
Laut SERA.5005 Buchstabe f (im deutschen Luftrecht umgesetzt in §37 der LuftVO) muss eine Mindesthöhe von 500 ft (150 m) über dem Boden oder Wasser oder 500 ft über dem höchsten Hindernis in einem Umkreis von 150 m um das Luftfahrzeug eingehalten werden. Über Städten, anderen dicht besiedelten Gebieten und Menschenansammlungen im Freien sind es sogar 1000 ft über dem höchsten Hindernis innerhalb eines Umkreises von 600 m um das Luftfahrzeug. Diese Höhen dürfen nur bei Start und Landung unterschritten werden. Segelflugzeuge, Hängegleiter und Gleitschirme, für die es bauartbedingt notwendig ist, dürfen die Mindestflughöhe unterschreiten. Dies könnt ihr auch im Luftfahrthandbuch AIP VFR in Kapitel ENR 1-16 noch einmal nachlesen.
Wenn man nun die MEF mit der Sicherheitsmindesthöhe addiert, bekommt man eine sichere Flughöhe. Natürlich muss auch die Luftraumstruktur noch berücksichtigt werden. Aber gerade in unerwarteten Abweichungen einer geplanten Flugroute ist der Wert eine sehr hilfreiche Angabe für einen weiterhin sicheren Flug.
Die Darstellung der MEF findet man nur auf der ICAO-Karte und den Europa-Karten der DFS. Karten anderer Hersteller zeigen direkt die Sicherheitsflughöhe an. Dort ist direkt der höchste Punk zuzüglich eines Sicherheitsabstandes von 1.000 bzw. 2.000 ft angegeben.
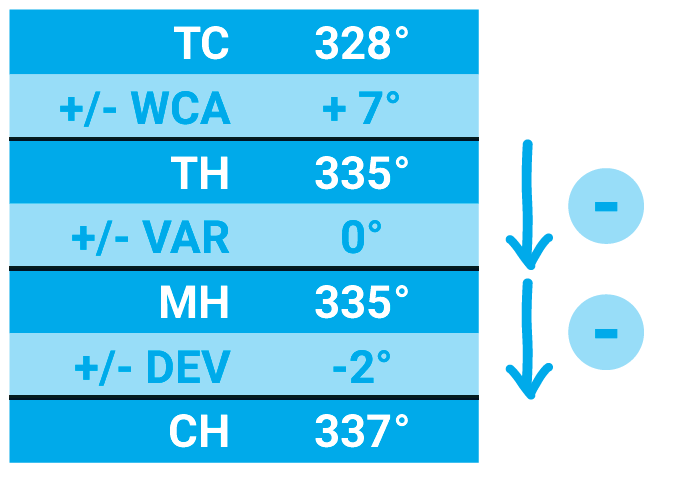

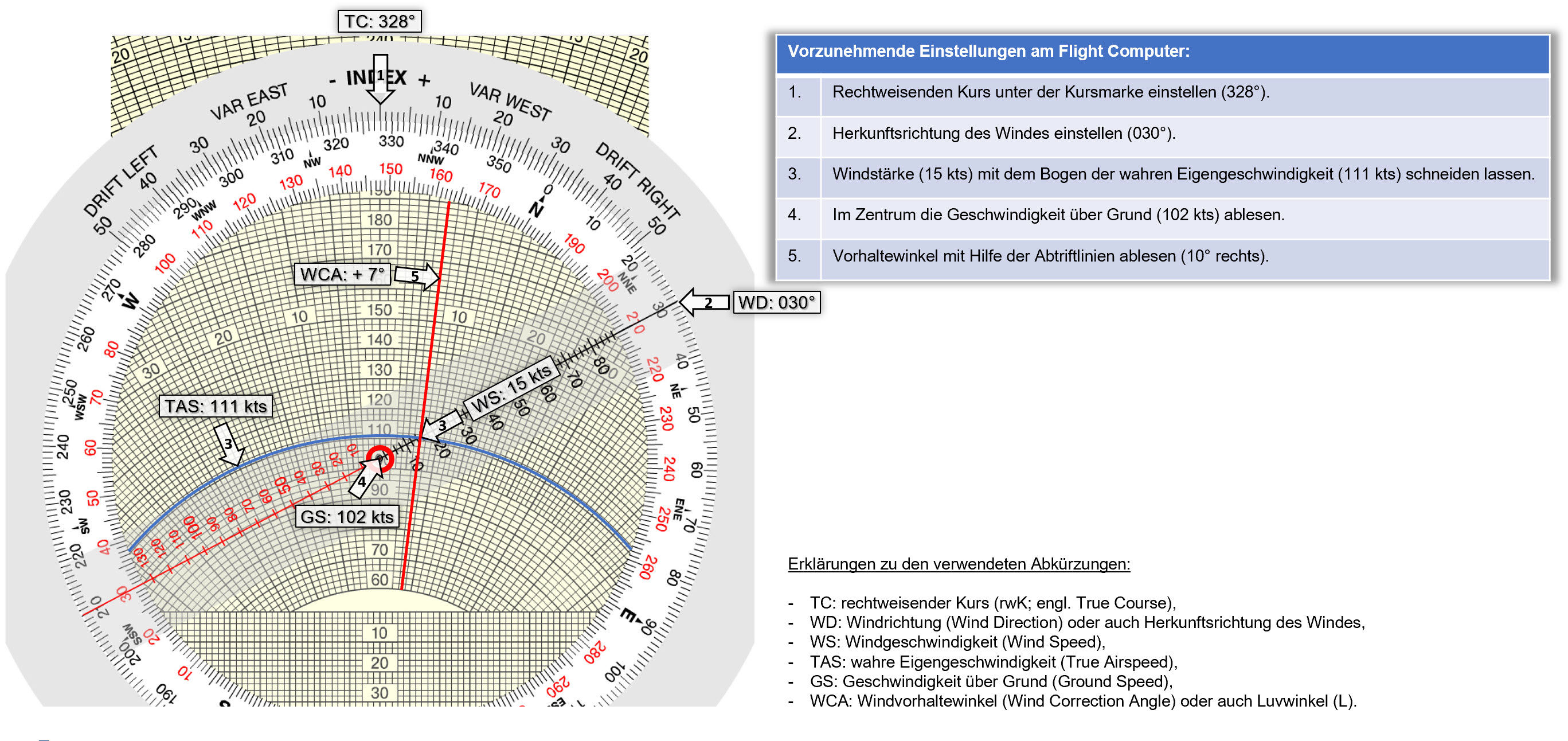









 Maximum Elevation Figure lässt sich übersetzen mit „größter Höhenwert“. Für die Ermittlung dieses Wertes gibt es zwei Rechenwege: die Höhenpunkt- und die Hindernisauswertung.
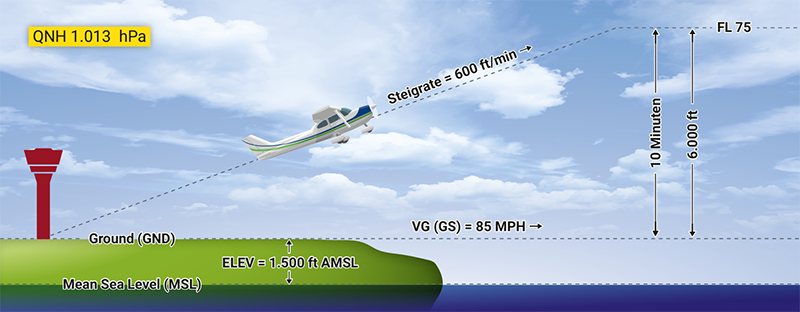
Maximum Elevation Figure lässt sich übersetzen mit „größter Höhenwert“. Für die Ermittlung dieses Wertes gibt es zwei Rechenwege: die Höhenpunkt- und die Hindernisauswertung.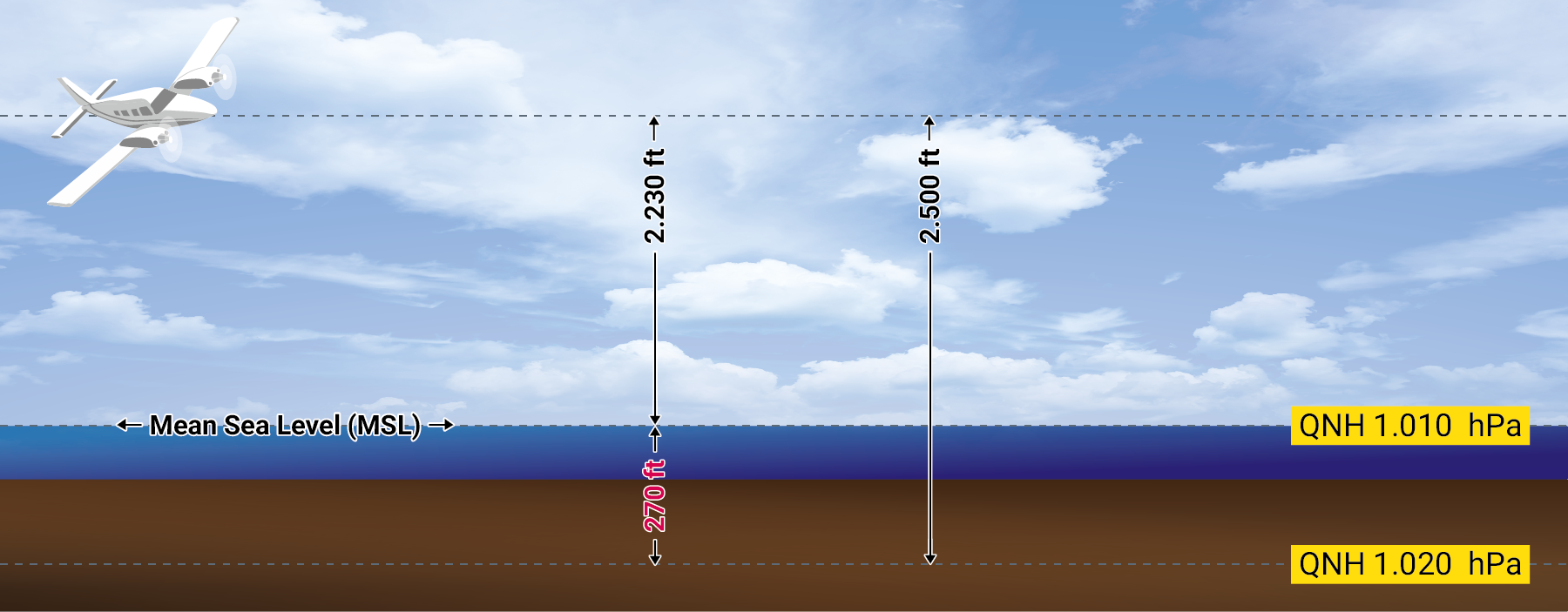
 Der Höhenmesser im Luftfahrzeug zeigt die Höhe über den Luftdruckwert an, der am Höhenmesser im Bezugsdruckfenster eingestellt wurde.
Der Höhenmesser im Luftfahrzeug zeigt die Höhe über den Luftdruckwert an, der am Höhenmesser im Bezugsdruckfenster eingestellt wurde.